Гистограммы
Гистограмма - массив столбиков длины $1$ и высоты $a_i$.
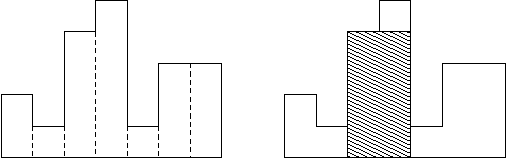
Наибольший прямоугольник, лежащий целиком “в гистограмме”.
Если $a_i$ - высота столбика $i$, то надо найти такие $x_1, x_2$ и $y$, что $a_i \geq y$ для всех $x_1 \leq i \leq x_2$, и $(x_2-x_1)*y$ максимально.
Эту задачу можно решить одним проходом с помощью стека.
Давайте будем идти по массиву столбцов и поддерживать лесенку из столбиков - максимальный набор столбиков, что для него в каждый момент времени:
- Столбцы упорядочены по номеру.
- Столбцы возрастают по высоте.
- Последний из рассмотренных столбцов является последним элементом стека.
Эту лесенку очень легко поддерживать с помощью стека - когда мы хотим добавить очередной столбик, нам просто надо удалять столбики, пока они не меньше текущего.
Оказывается, чтобы узнать ответ, надо просто каждый раз, когда мы удаляем столбик, посмотреть, какую площадь имеет прямоугольник, который упирается в этот столбец.
Его высоту мы знаем - она равна высоте столбца. Его левая граница имеет координату x, равную x-координате последнего столбика в стеке перед удаляемым, увеличенной на один.
Его правая координата - текущий столбец. А зная эти три величины, мы легко можем посчитать его площадь, после чего обновить ответ.
Остаётся только показать, что таким образом мы обработаем все нужные прямоугольники. Действительно, каждый потенциально подходящий прямоугольник сверху упирается хотя бы в один столбец, иначе его верхнюю границу можно было бы поднять на 1.
Раз для каждого интересного прямоугольника есть столбец, в который он упирается, то каждый интересный прямоугольник будет учтён хотя бы один раз.
Очевидно, что такой алгоритм будет иметь асимптотику $O(n)$ хотя бы потому, что каждый столбик мы только один раз добавим и один раз удалим.
Что касается реализации - может быть полезно положить в конец массива фиктивный нулевой элемент, чтобы в конце автоматически удалились все столбцы (если не удалить столбцы в конце, то какие-то прямоугольники не будут рассмотрены и ответ может быть неверным).
Для прямоугольника
Данный алгоритм позволяет, помимо прочего, решать задачу поиска наибольшего прямоугольника белого цвета на прямоугольном поле, покрашенном в белый и чёрный.
Для этого надо посчитать для каждой клетки количество белых сверху (это можно сделать за $O(1)$ для клетки, если использовать уже посчитанное значение для клетки сверху). После этого перебрать строку, которая будет нижней границей гистограммы, и для нее решить предыдущую задачу. Потом взять максимум по всем ответам.
Ясно, что асимптотика данного алгоритма - $O(nm)$, и меньше точно не получится, ведь это - размер прямоугольника.
Минимум на окне с помощью 2-х стеков
Стек с поддержанием минимума
Для поддержания минимума на стеке можно создать не стек элементов, а стек пар вида: элемент и минимум среди тех элементов, которые были добавлены раньше.
При добавлении элемента надо задавать минимум для него как минимум из элемента и минимума последнего из элементов в стеке. При удалении элемента ничего особенного делать не нужно.
Таким образом у нас получается стек, который помимо стандартных операций позволяет за $O(1)$ узнать минимум среди всех элементов в стеке.
Поддержание минимума на окне
Для массива $a$ назовем окном текущий подмассив размером $k$, то есть $a[i…i+k]$. При увеличении $i$, окно будет как бы сдвигаться, пробегая все возможные подмассивы такой длины.
Мы будем использовать наш стек с поддержанием минимума, причём нам понадобится еще один обычный стек.
Стек с поддержанием минимума будет началом окна - из него мы будем удалять элементы. Другой обычный стек будет концом окна - туда мы будем только класть элементы (тогда можно поддерживать минимум в нем в одной переменной).
Легко заметить, что для поиска минимума достаточно посмотреть на значение минимумов в обоих стеках и взять меньший.
Опишем механизм, по которому мы будем перекладывать элементы из “хвостового” стека в “головной”:
- Новые элементы будем добавлять в “хвостовой” стек
- Если хотим удалить элемент из “головного” стека и он оказался пустой, переложим все элементы из “хвостового” стека.
Легко показать, что последовательность элементов при этом не нарушится.
Так же заметим, что в “хвостовой” стек мы либо добавляем элементы, либо очищаем его полностью, а значит одной переменной для поддержания в нем минимума достаточно.
Несмотря на наивные перекладывания большого количества элементов из хвоста в голову, средняя асимптотика удаления элемента будет равна $O(1)$.
Действительно, каждый элемент в худшем случае один раз будет положен в хвост, потом один раз переложен в голову и затем один раз удалён. Каждая из этих операций работает за $O(1)$, а значит, и средняя асимптотика удаления составит $O(1)$.
Такая асимптотика, когда в среднем тратится $O(1)$, но на отдельные операции может тратиться больше, называется амортизированной асимптотикой.